Como Explicar Fracciones A Niños De Tercero De Primaria – ¿Estás buscando una manera fácil y divertida de explicar las fracciones a los niños de tercer grado? ¡No busques más! Esta guía paso a paso te proporcionará las herramientas y estrategias que necesitas para ayudar a tus alumnos a dominar este concepto matemático esencial.
Prepárate para transformar el aprendizaje de las fracciones en una experiencia emocionante y significativa.
Las fracciones son una parte integral de nuestras vidas diarias, desde medir ingredientes hasta calcular descuentos. Al comprender las fracciones, los niños pueden desarrollar habilidades esenciales para resolver problemas y tomar decisiones informadas.
Definición de fracciones: Como Explicar Fracciones A Niños De Tercero De Primaria

Las fracciones son una forma de representar partes de un todo. Están formadas por dos números: el numerador y el denominador.
El numerador es el número que está arriba y nos indica cuántas partes del todo tenemos. El denominador es el número que está abajo y nos indica en cuántas partes está dividido el todo.
Ejemplo de fracciones
Por ejemplo, la fracción 1/2 significa que tenemos una parte de un todo que está dividido en dos partes iguales. La fracción 3/4 significa que tenemos tres partes de un todo que está dividido en cuatro partes iguales.
Representación de fracciones
Existen varias formas de representar fracciones, cada una con sus ventajas y desventajas. Las más comunes son:
- Círculos divididos:Una fracción se puede representar dividiendo un círculo en partes iguales y sombreando la cantidad de partes indicadas por el numerador.
- Rectángulos:Una fracción se puede representar dividiendo un rectángulo en partes iguales y sombreando la cantidad de partes indicadas por el numerador.
- Números decimales:Una fracción se puede representar como un número decimal dividiendo el numerador por el denominador.
Representación de fracciones como números decimales
Para representar una fracción como un número decimal, se divide el numerador por el denominador. Por ejemplo, 1/2 se representa como 0,5 porque 1 dividido por 2 es 0,5.
Comparación de fracciones
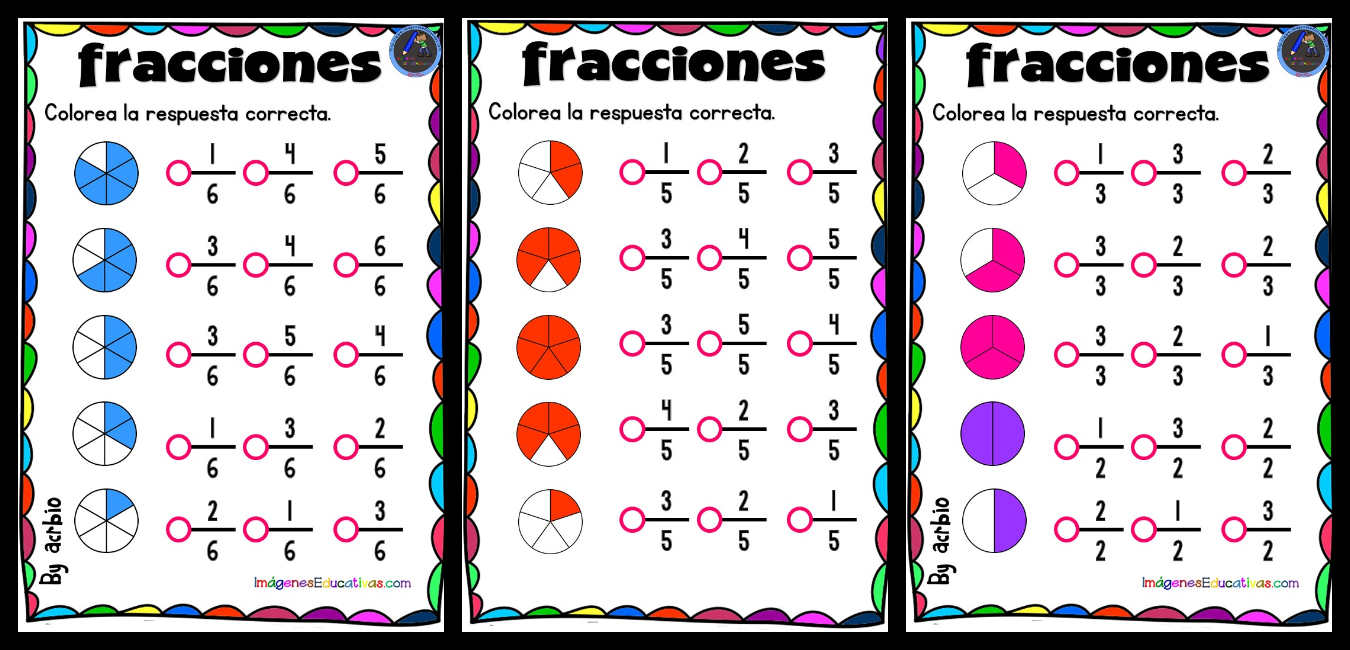
Para comparar fracciones, necesitamos entender su valor. Las fracciones representan partes de un todo, y cuanto mayor sea el denominador, más pequeñas serán las partes.
Fracciones con el mismo denominador, Como Explicar Fracciones A Niños De Tercero De Primaria
Cuando las fracciones tienen el mismo denominador, podemos compararlas directamente. La fracción con el numerador más grande es mayor.
- 1/4 es menor que 2/4 porque 1 es menor que 2.
- 3/5 es mayor que 2/5 porque 3 es mayor que 2.
Fracciones con diferentes denominadores
Cuando las fracciones tienen diferentes denominadores, necesitamos convertirlas a fracciones equivalentes con el mismo denominador. Para hacer esto, multiplicamos el numerador y el denominador de cada fracción por un número que haga que los denominadores sean iguales.
Por ejemplo, para comparar 1/2 y 3/4:
- Multiplicamos 1/2 por 2/2 (1 x 2 = 2, 2 x 2 = 4), obteniendo 2/4.
- 3/4 ya tiene un denominador de 4, por lo que no es necesario convertirlo.
- Ahora podemos comparar 2/4 y 3/4. Como 3 es mayor que 2, 3/4 es mayor que 2/4.
Operaciones con fracciones
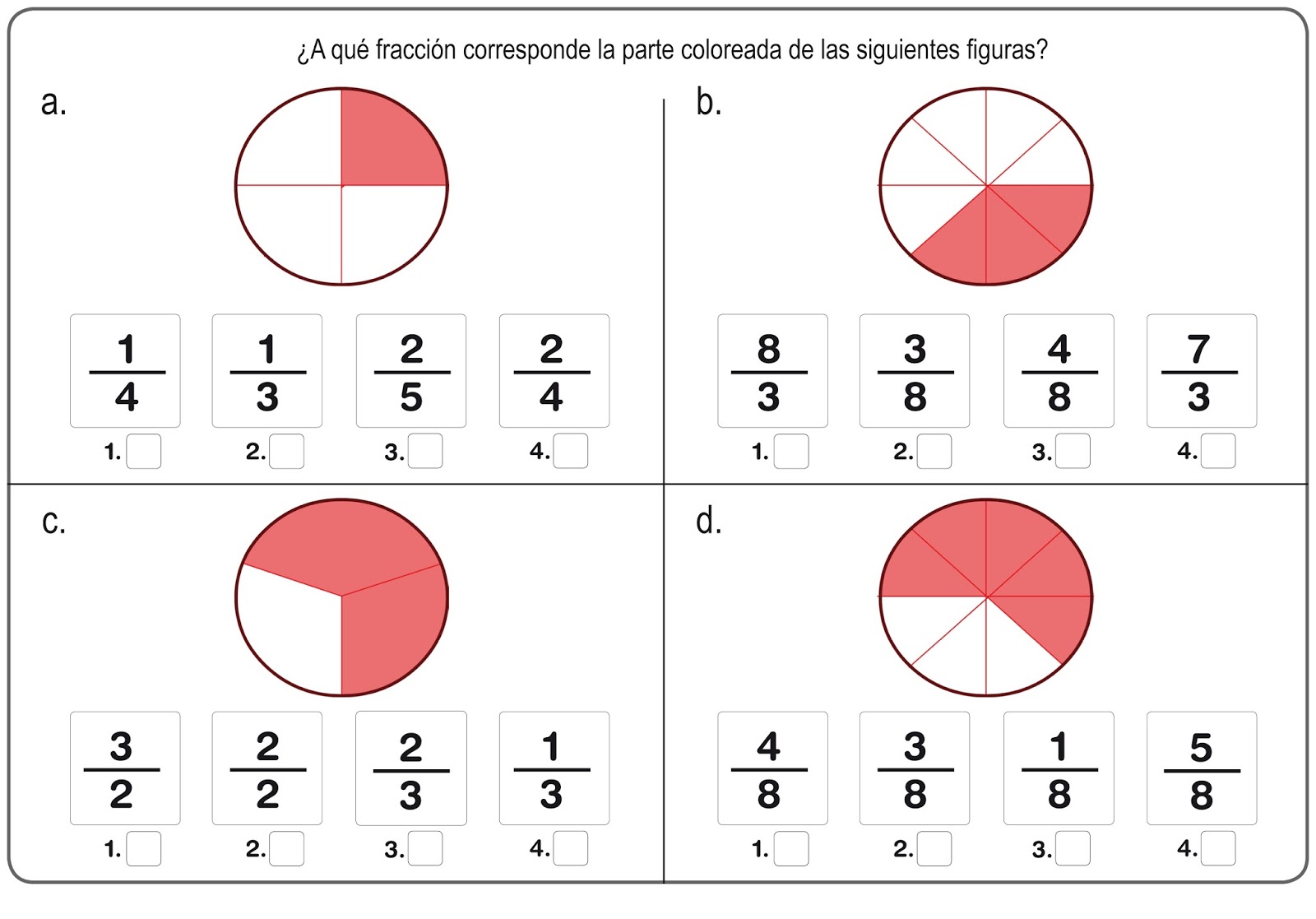
Las fracciones son partes de un todo. Para sumar o restar fracciones con el mismo denominador, simplemente suma o resta los numeradores y mantén el mismo denominador. Por ejemplo, 1/2 + 1/2 = 2/2. Para multiplicar fracciones, multiplica los numeradores y los denominadores.
Por ejemplo, 1/2 x 1/2 = 1/4. Para dividir fracciones, invierte la segunda fracción y multiplica. Por ejemplo, 1/2 ÷ 1/2 = 1/2 x 2/1 = 2/2 = 1.
Suma y resta de fracciones con el mismo denominador
Para sumar o restar fracciones con el mismo denominador, suma o resta los numeradores y mantén el mismo denominador.
- 1/2 + 1/2 = 2/2
- 3/4 – 1/4 = 2/4
Multiplicación de fracciones
Para multiplicar fracciones, multiplica los numeradores y los denominadores.
- 1/2 x 1/2 = 1/4
- 2/3 x 3/4 = 6/12 = 1/2
División de fracciones
Para dividir fracciones, invierte la segunda fracción y multiplica.
- 1/2 ÷ 1/2 = 1/2 x 2/1 = 2/2 = 1
- 2/3 ÷ 3/4 = 2/3 x 4/3 = 8/9
Aplicaciones de las fracciones en la vida cotidiana
Las fracciones son herramientas poderosas que utilizamos en innumerables situaciones cotidianas. Nos ayudan a medir ingredientes en recetas, calcular descuentos y resolver muchos otros problemas prácticos.
Cálculo de ingredientes
Las fracciones son esenciales en las recetas. Por ejemplo, si una receta requiere 1/2 taza de leche, debemos medir media taza de leche. Las fracciones nos permiten dividir con precisión los ingredientes para obtener las proporciones correctas.
Mediciones
Las fracciones también se utilizan para realizar mediciones precisas. Por ejemplo, si necesitamos medir una distancia de 3/4 de pulgada, usamos una regla o cinta métrica para dividir la pulgada en cuatro partes iguales y luego medir tres de esas partes.
Cálculo de descuentos
Las fracciones nos ayudan a calcular descuentos y rebajas. Por ejemplo, si un artículo tiene un descuento del 25%, debemos multiplicar el precio original por 3/4 (1 – 0,25) para obtener el precio con descuento.
¡Enhorabuena! Ahora tienes las herramientas y el conocimiento para explicar las fracciones a los niños de tercer grado de manera efectiva. Recuerda utilizar representaciones visuales, comparaciones prácticas y ejemplos de la vida real para hacer que el aprendizaje sea atractivo y comprensible.
¡Con paciencia y entusiasmo, puedes ayudar a tus alumnos a desarrollar una comprensión sólida de este concepto fundamental!
