Ejercicios De Union De Conjuntos Para Niños De Primaria – ¡Sumérgete en el fascinante mundo de los Ejercicios de Unión de Conjuntos para Niños de Primaria! Explora los conceptos básicos, aprende las operaciones y descubre aplicaciones prácticas con nuestra guía integral que te cautivará desde el primer momento.
Adéntrate en el universo de los conjuntos y descubre sus propiedades únicas. A través de ejemplos cotidianos, entenderás la unión de conjuntos, su intersección y su diferencia. Los diagramas de Venn te ayudarán a visualizar estas operaciones de forma clara y sencilla.
Conceptos básicos de conjuntos

Los conjuntos son un concepto fundamental en matemáticas que se utilizan para organizar y clasificar elementos. Un conjunto es una colección de elementos bien definidos y distintos.Las propiedades básicas de los conjuntos incluyen:
-
-*Claridad
Los elementos del conjunto deben estar claramente definidos y no pueden repetirse.
-*Distinción
Cada elemento del conjunto es único y no puede aparecer más de una vez.
-*Orden
Los elementos del conjunto no tienen un orden específico.
Ejemplos de conjuntos en la vida cotidiana
Los conjuntos se encuentran en muchos aspectos de la vida cotidiana, por ejemplo:
-
-*Conjunto de frutas
Manzanas, plátanos, naranjas
-*Conjunto de números pares
2, 4, 6, 8, …
-*Conjunto de estudiantes en una clase
Juan, María, Pedro, …
Operaciones con conjuntos
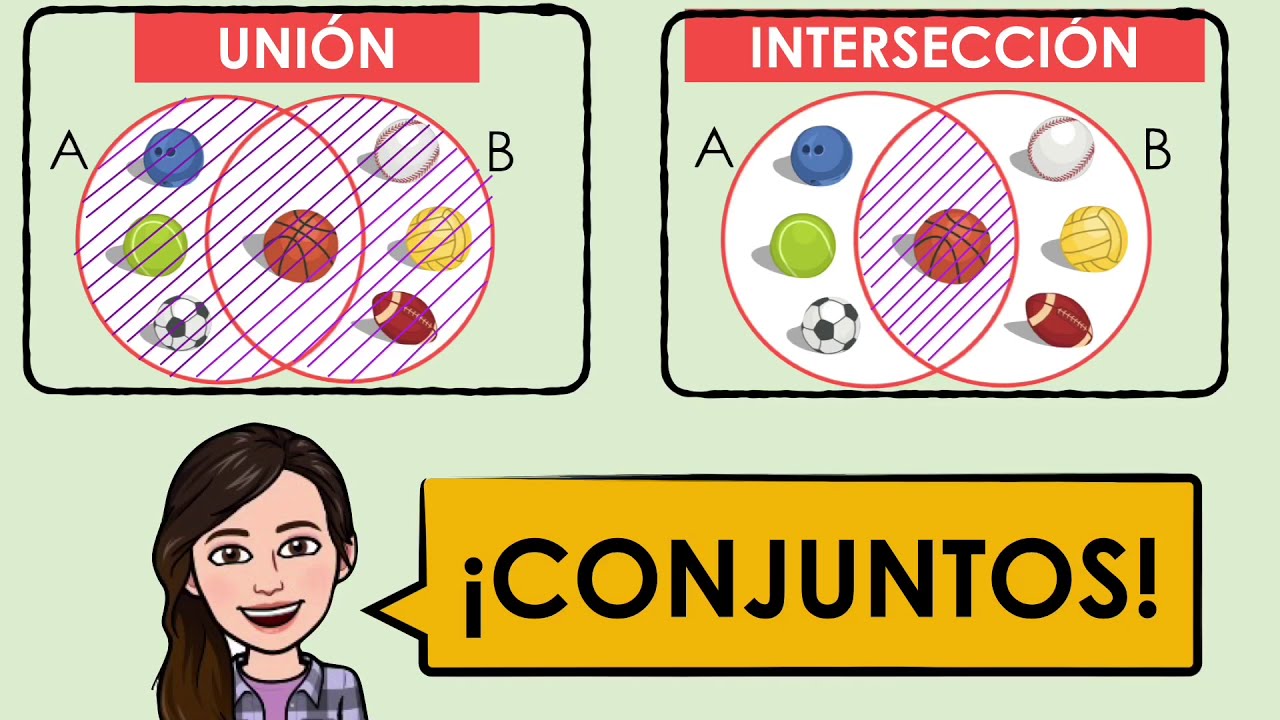
En matemáticas, los conjuntos son grupos de elementos bien definidos. Las operaciones con conjuntos son operaciones que permiten combinar o manipular conjuntos para obtener nuevos conjuntos. Las operaciones básicas con conjuntos son unión, intersección y diferencia.
Unión
La unión de dos conjuntos, A y B, es un nuevo conjunto que contiene todos los elementos que están en A o en B, o en ambos. Se denota como A ∪ B.Por ejemplo, si A = 1, 2, 3 y B = 3, 4, 5, entonces A ∪ B = 1, 2, 3, 4, 5.
Intersección
La intersección de dos conjuntos, A y B, es un nuevo conjunto que contiene solo los elementos que están tanto en A como en B. Se denota como A ∩ B.Por ejemplo, si A = 1, 2, 3 y B = 3, 4, 5, entonces A ∩ B = 3.
Diferencia
La diferencia de dos conjuntos, A y B, es un nuevo conjunto que contiene los elementos que están en A pero no en B. Se denota como A
B.
Por ejemplo, si A = 1, 2, 3 y B = 3, 4, 5, entonces A
B = 1, 2.
La siguiente tabla resume las operaciones con conjuntos:
| Operación | Símbolo | Definición |
|---|---|---|
| Unión | A ∪ B | Conjunto de todos los elementos en A o en B, o en ambos |
| Intersección | A ∩ B | Conjunto de elementos que están tanto en A como en B |
| Diferencia | A
|
Conjunto de elementos que están en A pero no en B |
Diagramas de Venn para conjuntos
Los diagramas de Venn son una herramienta visual que nos ayuda a representar y entender las relaciones entre conjuntos. Son círculos que se superponen para mostrar los elementos que comparten y los que no.
Cómo utilizar los diagramas de Venn
Para utilizar un diagrama de Venn, dibujamos un círculo para cada conjunto. Los elementos que pertenecen a ambos conjuntos se representan en el área donde los círculos se superponen. Los elementos que pertenecen solo a un conjunto se representan en las áreas fuera de la superposición.
Ejemplo de diagrama de Venn
Dibujemos un diagrama de Venn para representar los conjuntos A y B, donde A es el conjunto de números pares y B es el conjunto de números menores que 5.El área sombreada representa los elementos que están en ambos conjuntos, es decir, los números pares menores que 5. En este caso, son 2 y 4.
Ejercicios prácticos de unión de conjuntos
¡Ahora es el momento de poner en práctica tus habilidades con los conjuntos! Te proponemos una serie de ejercicios de unión de conjuntos diseñados especialmente para niños de primaria. Estos ejercicios están organizados en orden de dificultad creciente, así que no te preocupes si al principio no puedes resolverlos todos.
¡Con un poco de práctica, te convertirás en un experto en unión de conjuntos!
Ejercicios de dificultad baja
- El conjunto A contiene los números del 1 al 5. El conjunto B contiene los números del 3 al 7. Encuentra la unión de los conjuntos A y B.
- El conjunto C contiene las letras “a”, “e”, “i”, “o”, “u”. El conjunto D contiene las letras “a”, “b”, “c”, “d”, “e”. Encuentra la unión de los conjuntos C y D.
Ejercicios de dificultad media, Ejercicios De Union De Conjuntos Para Niños De Primaria
- El conjunto E contiene los números pares del 1 al 10. El conjunto F contiene los números impares del 1 al 10. Encuentra la unión de los conjuntos E y F.
- El conjunto G contiene los animales que viven en el agua. El conjunto H contiene los animales que viven en la tierra. Encuentra la unión de los conjuntos G y H.
Ejercicios de dificultad alta
- El conjunto I contiene los múltiplos de 3 menores que 20. El conjunto J contiene los múltiplos de 5 menores que 20. Encuentra la unión de los conjuntos I y J.
- El conjunto K contiene los factores de 12. El conjunto L contiene los factores de 18. Encuentra la unión de los conjuntos K y L.
¡Esperamos que disfrutes resolviendo estos ejercicios y que te ayuden a mejorar tus habilidades con los conjuntos! Recuerda que la práctica es la clave del éxito, así que no te desanimes si no puedes resolver todos los ejercicios a la primera.
¡Sigue practicando y pronto serás un maestro de los conjuntos!
Aplicaciones de la unión de conjuntos
La unión de conjuntos tiene numerosas aplicaciones en diversos ámbitos, desde las matemáticas y la informática hasta la vida cotidiana. Esta operación nos permite combinar elementos de diferentes conjuntos para crear un nuevo conjunto que contiene todos los elementos de los conjuntos originales.
La unión de conjuntos es esencial en la vida diaria, ya que nos ayuda a organizar y gestionar información. Por ejemplo, si tenemos una lista de amigos en Facebook y una lista de seguidores en Twitter, podemos utilizar la unión de conjuntos para crear una lista completa de todas las personas con las que nos relacionamos en las redes sociales.
En matemáticas
- Resolver ecuaciones y sistemas de ecuaciones.
- Demostrar teoremas y propiedades.
- Construir nuevos conjuntos con propiedades específicas.
En informática
- Diseñar bases de datos y sistemas de gestión de información.
- Procesar y analizar grandes conjuntos de datos.
- Crear algoritmos eficientes para resolver problemas complejos.
En la vida cotidiana
- Planificar eventos y reuniones.
- Gestionar proyectos y tareas.
- Organizar información y recursos.
¡La unión de conjuntos no solo es un concepto matemático, sino una herramienta esencial en nuestra vida diaria! Desde la planificación de eventos hasta la resolución de problemas, la comprensión de las uniones de conjuntos te empoderará para tomar decisiones informadas y navegar por el mundo con confianza.
Common Queries: Ejercicios De Union De Conjuntos Para Niños De Primaria
¿Qué es un conjunto?
Un conjunto es una colección de elementos distintos que comparten una característica común.
¿Qué es la unión de conjuntos?
La unión de dos conjuntos es un nuevo conjunto que contiene todos los elementos que pertenecen a cualquiera de los conjuntos originales.
¿Cómo se utilizan los diagramas de Venn para representar conjuntos?
Los diagramas de Venn utilizan círculos superpuestos para representar conjuntos. Los elementos que comparten ambos conjuntos se encuentran en la región superpuesta.
